Palavras chaves: formulação, balanceamento, NRC, RLM, Exigências, Bovinos, Aves, Suínos, Equídeos, Equínos, sal mineral, suplemento, mineral, ração, núcleo, concentrado, premix, animal, fazenda, confinamento, leite, corte, bezerro, vaca, boi, novilha, garrote
Quais são os métodos que podemos utilizar para formular uma ração? E um sal mineral? Ou um proteinado?
O mais simples é pelo método de tentativa e erro. Neste método é necessário você saber as particularidades dos alimentos, como inclusão ideal em uma dieta e quais são seus limitantes.
⦁ Neste procedimento também é necessário saber os níveis de garantia dos ingredientes a serem utilizados para chegar ao objetivo final.
⦁ Exemplo:
⦁ Ração de leite com 24% de PB
⦁ Onde o Farelo de Soja tem 46% PB (Proteína bruta) e o Milho tem 8% de PB na MN (Matéria Natural)
⦁ Iremos fazer uma regra de três básica, onde iremos “chutar” que 44% de Farelo de Soja será o ideal.
PB %
46 —–100
X —— 44
X = 46*44/100
farelo de soja irá contribuir com X = 20,24% PB
Considerando que temos 100%, porém, 44% será de farelo de soja e 3% será de um núcleo mineral, restará então 53% para o milho.
PB %
8 —–100
X —— 53
X = 53*8/100
Milho irá contribuir com X = 4,24% PB
Neste exemplo o núcleo é apenas de mineral, assim não irá contribuir com a PB do produto, então Milho + Farelo de Soja + Núcleo = 100%, fica 20,24 + 4,24 = 24,48% de Proteína Bruta nesta mistura.
Se você conseguiu entender, ficará fácil de fazer com mais alimentos!
Vamos para um método mais técnico, o Quadrado de Pearson, é um método bem simples e que lhe trás um resultado exato. Método que permite o cálculo das proporções de dois componentes de uma mistura a fim de atender um nível de nutriente desejado.
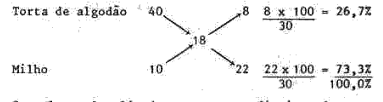
Não entendeu? Então eu vou te explicar!
Neste exemplo foi considerado que a Torta de Algodão tem 40% de PB e o Milho 10%, no centro do Quadrado, colocamos qual o nível que desejamos, no exemplo buscamos uma ração com 18% de PB.
Após a definição, é feito a subtração de forma cruzada, 40-28 = 22 e 18-10 = 8. Após este momento se soma os resultados, 8+ 22 = 30. Agora temos 30 é igual a 100%, então faremos a proporção, se 30 é 100%, 8 é quanto? = 26,7% de Torta de Algodão. Se 30 é 100% 22 é quanto? = 73,3% de Milho.
Quer tirar a prova?
26,7% * 40 = 10,68%
73,3% * 10 = 7,33%
SOMA = 18,01%
Legal né? Vamos dificultar mais um pouco? Vamos lá
Vamos formular uma ração com 24% de PB, só que ela terá 1% de ureia e 3% de núcleo.
Para começarmos vamos definir aqui as variáveis.
M = Milho, FS = Farelo de Soja, U = Ureia e NC = Núcleo
M + FS + U + NC = 100
M + FS + 1 + 3 = 100
M + FS = 96
M + FS + U + NC = 24%
M + FS + (281*(1/100) + 0 = 24
M + FS = 21,19
Então já chegamos que milho e farelo de soja somam 96% da formulação e que faltam 21,19% de PB para chegarmos aos 24% desejados.
Milho 8 23,93 38_______ 96
23,93_____ M = 60,53
Farelo de soja 46 14,07 38_______96
38 14,07_____ FS= 35,54
Resultado:
M + FS + U + NC = 100%
35,54 + 60,53 + 1 + 3 = 100%
M + FS + U + NC = 24%
4,85 + 16,35 + 2,81 + 0 = 24%
Foi fácil né? Agora você consegue formular com quantos alimentos quiser!
Vamos para mais uma forma de cálculo? Com Função Algébrica!
⦁ Consiste em formar um sistema de equações com tantas incógnitas quantos forem os ingredientes utilizados.
M + FS + U + NC = 100
(MPB) + (FSPB) + (U*PB) + NC = 18
M + FS + 1 + 3 = 100
(M0,08) + (FS0,46) + 2,81 + 0 = 18
M + FS =100 – 4
M = 96 – F.S
(M0,08) + (F.S0,46) = 18 – 2,81
(M0,08) + (F.S0,46) = 15,19
SUBSTITUINDO A VARIÁVEL:
((96–FS)0,08) + (FS0,46) = 15,19
(7,68-FS0,08) + (FS0,46) = 15,19
FS*0,38 = 7,5
FS = 19,73
M = 96 – FS
M = 96-19,73
M = 76,27
Fácil né?? Formulação é matemática!
E para Finalizar temos o método linear, neste método é necessário o uso do excel ou programas de formulação. Segue tabela em excel para dowload. E conheça nosso software e aplicativo.

